Question

I know it's easy but, I'm thinking of different ways of doing it.

Answer 1

9 students

Explanation:

Every 8th person that entered the cinema received a free ticket.

The number of students who entered in the first hour = 76.

The first person given a ticket was the 8th person.

To calculate the number of persons who received a free ticket, we can view this problem as an arithmetic sequence in which:

• The first term = 8

,

• The last term = 76.

,

• The common difference (every 8th person) = 8.

Using the formula for the last term of an arithmetic sequence, we have:

`\begin{gathered} l=a+(n-1)d_{} \\ 76=8+8(n-1) \end{gathered}`

Our goal is to find n, the number of students.

`\begin{gathered} 76=8+8n-8 \\ 76=8n \\ n=(76)/(8) \\ n=9.5 \end{gathered}`

Since the number of students that entered in the first hour is not more than 76, we have that:

`\begin{gathered} n\le9.5 \\ \implies n=9 \end{gathered}`

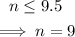
9 students received a free ticket.