Let x be the length of the rectangle and y be the width of the rectangle, then we can set the following equations:
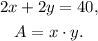
Solving the first equation for x we get:
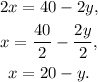
Substituting x=20-y in the second equation we get:
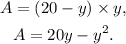
Now, we will use the first and second derivative criteria to find the maximum.
The first and second derivatives are:
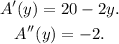
Since the second derivative is a negative number that means that A(y) reaches a maximum when A´(y)=0.
Solving A´(y)=0 for y we get:
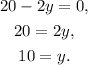
Now, substituting y=10 in x=20-y, we get:

Answer:
Length 10 yards.
Width 10 yards.