The working equation when dealing with problems regarding compounded interest is

where A is the future value, P is the principal value, r is the annual rate, and n is the number of compounding periods.
The problem compounds quarterly, hence, we have n = 4.
We derive the working equation to solve for t, as follows:
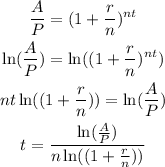
Substitute the values of A, P, n, and r on the derived equation above and solve for t, we get
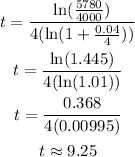
Therefore, the $4000 investment grows to $5780 in 9.25 years.