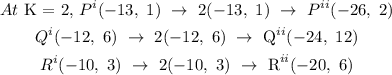SOLUTION
We are told to translate; (x, y) to (x -8, y). This means we have to add - 8 to each value of x in P(-5,1), Q(-4,6), and R(-2,3).
In P(-5,1), x = -5 and y = 1
In Q(-4,6), x = -4 and y = 6 and
In R(-2,3), x = -2 and y = 3
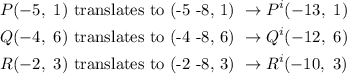
For the dilation centered at the origin k =2, simply multiply the value of k, which is 2 into the translations.