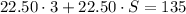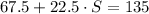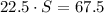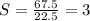Question

8.) Antwoine cuts 3 lawns in his neighborhood on Friday and more on Saturday.He earns $22.50 for each lawn cut. His total earning for both days is $135.How many lawns did he cut on Saturday?

Answer 1

The first step to solve this problem is to realize that this information can be "translate" into a linear system of two equations. Let's denote by F the number of lawns he cuts on Fridays and let's denote by S the corresponding on Saturdays. So we have

`22.50\cdot F+22.50\cdot S=135`
`F=3`

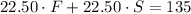
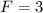
Replacing the value of F into the first equation we get

`22.50\cdot3+22.50\cdot S=135`
`67.5+22.5\cdot S=135`
`22.5\cdot S=67.5`
`S=(67.5)/(22.5)=3`