Question

In a study of randomly selected women science majors, the following data were obtained on two groups, those who left their profession within a few months after graduation (leavers) and those who remained in their profession after they graduated (stayers). Test the claim that those who stayed had a higher science grade point average than those who left. Use α = 0.05.

Answer 1

X₁: science GPA for those who left their profession after graduation

X₂ science GPA for those who remained in their profession after graduation.

The working hypothesis is that the GPA of those who stayed is higher than those who left.

Which is the same as saying that the GPa of those who left is less than those who stayed.

μ₁ represents the population mean of the science GPA of those who left.

μ₂ represents the population mean of the science GPA of those who remained.

Part one

You can express the working hypothesis as follows:

`\mu_1<\mu_2`

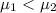
The hypothesis does not include the equal sign, so this hypothesis can be considered as the alternative hypothesis.

The null hypothesis of this test will be the complement of the alternative hypothesis, and always carries the equal sign within. So if the alternative hypothesis states that "the mean of the leavers is less than the mean of the stayers", then the null hypothesis will be that "the mean of the leavers is greater than or equal to the mean of the stayers" you can symbolize this as:

`\mu_1\ge\mu_2`

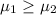
Since the null hypothesis carries the equal sign you can also write it as:

`\mu_1=\mu_2`

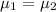
Both options are equally valid.

So, the second answer is null hypothesis.

Part two

Considering that we are studying the population means of two normal variables and that we know the population standard deviation for both populations, the test statistic to use is the standard normal for the difference of means which is defined as follows:

`Z=\frac{(\bar{X_1}-\bar{X_2})-(\mu_1-\mu_2)}{\sqrt[]{(\sigma^2_1)/(n_1)+(\sigma^2_2)/(n_2)}}N(0,1)`

Subindex 1 indicates the values corresponding to the "leavers":

X₁bar= 3.16

n₁= 103

σ₁= 0.52 → σ₁²= 0.2704

Subindex 2 indicates the values corresponding to the "stayers":

X₂bar= 3.28

n₂= 225

σ₂= 0.46 → σ₂²= 0.2116

Under the null hypothesis both population means are equal, which means that their difference is equal to zero:

If μ₁ = μ₂, then μ₁ - μ₂ = 0

Replace all values on the formula to determine the Z-value under the null hypothesis, i.e. the test statistic: