Recall that:
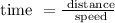
Let Victoria's speed be v.
Therefore, Victoria's resultant speed upstream is v - 4 and her resultant speed downstream is v + 4.
Hence the time of journey upstream is given by:
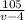
And the time of journey downstream is given by:
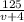
Since the time of journey upstream is the same as the time of journey downstream, it follows that:

Therefore, Victoria's speed is 46 mph