Given:
a logarithm is given as

Find:
we have to expand the given logarithm expressionusing properties of logarithm.
Step-by-step explanation:
we know from the properties of logarithm that

we will use above properties to expand the given logarithm expression as follows
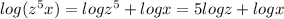
Therefore, the expansion of the given logarithm is 5 log(z)+ log(x)