Question

Hello can you explain to me how I should write this out please

Answer 1

`\text{Interquartile range = 2 lbs 1 oz}`

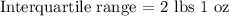
Here, we want to calculate the interquartile range

Mathematically, this is the difference between the lower quartile (1st quartile or 25th percentile) and the upper quartile (3rd quartile or 75th percentile)

We already have the numbers arranged from top to bottom

The count of numbers is 9 numbers

We have the first quartile as;

`((n+1))/(4)\text{ = }(10)/(4)\text{ = 2.5th which is 3rd term}`

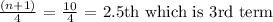
The third term here is the weight of baby Selena

The 3rd quartile can be calculated as;

`(3(n+1))/(4)\text{ = }(3(9+1))/(4)\text{ = 7.5 which is 8th term}`

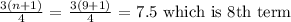
The 8th term is the weight of baby Me

The difference between these weights give the interquartile range as follows;

`\text{Interquartile range =Q}_3-Q_1\text{ = 8 lbs 2 oz - 6 lbs 1 oz = 2 lbs 1 oz}`