The function is given to be:
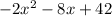
The object hits the ground when the function is equal to zero:
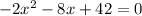
Solving the equation by factorization, we have:
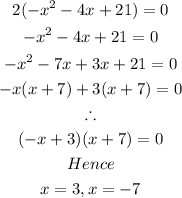
Since the time cannot be negative, then the time will be 3 seconds.
Therefore, it will take 3 seconds for the object to hit the ground.