Question

Find the values of x and y in the following right triangle. Enter square roots not decimals.

Answer 1

Recall the following trigonometric identities. If the legs of the right triangle have lengths a and b, the hypotenuse has length c, and the side a is adjacent to an angle θ, then:

`\begin{gathered} \sin \theta=(b)/(c) \\ \cos \theta=(a)/(c) \end{gathered}`

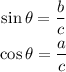
Then, for the given right triangle:

`\begin{gathered} \sin (30º)=(x)/(8) \\ \cos (30º)=(y)/(8) \end{gathered}`

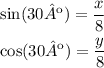
Then, x and y are given by the expressions:

`\begin{gathered} x=8\cdot\sin (30º)=8\cdot(1)/(2)=4 \\ y=8\cdot\cos (30º)=8\cdot\frac{\sqrt[]{3}}{2}=4\cdot\sqrt[]{3} \end{gathered}`

Therefore, the answers are:

`\begin{gathered} x=4\cdot\sqrt[]{3} \\ y=4 \end{gathered}`