Question

List the inverval(s) that the function is increasing.List the interval(s) on which the function is decreasing.list the interval(s) on which the function is constant. type each answer in interval notation

Answer 1

The graph of an increasing function has a positive slope. A line with a positive slope slants upward from left to right.

In this case, the graph of the function slants upward from left to right on the interval given by:

`(-\infty,-8)\cup(-3,-2)`

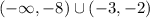
The graph of a decreasing function has a negative slope. A line with a negative slope slants downwared from left to right.

In this case, the graph of the function slants downward from left to right on the interval given by:

`(-8,-6)`

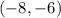
The graph of a constant function has a slope of zero. A line with a zero slope is horizontal and parallel to the x-axis.

In this case, the graph of the function is parallel to the x-axis on the interval given by:

`(-6,-3)\cup(-2,\infty)`

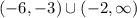
Therefore, the function is increasing on the interval (-∞, -8)∪(-3,-2), decreasing on the interval (-8, -6) and constant on the interval (-6, -3)∪(-2,∞)

.