Question

In a sample of 500 people 225 people could twist their tongues two people are selected at random from the sample without replacement Find the probability that both can twist their tonguesFind the probability that both can’t twist their tongues Answer the following problems using multiplication rule make sure to reduce your fraction

Answer 1

To obtain the probabilities asked about in the question, we proceed as follows:

Step 1: Recall the definition of the probability of any event E occuring, which is as follows:

`P(E)=(n(E))/(n(S))`

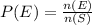
where:

n(E) = number of elements in set E

n(S) = number of elements in the entire sample space

Step 2: Identify the data given in the question, as follows:

We have that:

Total sample = 500 people

Tongue twisters = 225

Step 3: Interpret the question prompts, as follows:

a) Find the probability that both of the two people selected from the sample can twist their tongues.

To do this, we write out the probabilities associated with the first and second selection of such two people from the sample, as below:

- the probability associated with the first selection is:

`P(1st\text{ tongue twister) =}\frac{number\text{ of tongue twisters}}{\text{total numbe of sample space}}=(225)/(500)`

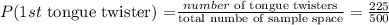
- the probability associated with the second selection is:

`P(2nd\text{ tongue twister) =}\frac{number\text{ of tongue twisters AFTER 1st selection}}{\text{total numbe of sample space after 1st selection}}=(224)/(499)`

Now, the the probability that both of the two people selected from the sample can twist their tongues is therefore:

`P(1st\text{ tongue twister) }*\text{ }P(2nd\text{ tongue twister)}`

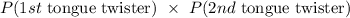
Thus:

`P(1st\text{ tongue twister) }*\text{ }P(2nd\text{ tongue twister) = }(225)/(500)*(224)/(499)\text{ = }(504)/(2495)`

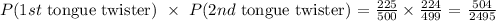
The answer is thus : 504/2495

b) Find the probability that both of the two people selected from the sample can NOT twist their tongues

To do this, we write out the probabilities associated with the first and second selection of such two people from the sample, as below:

- the probability associated with the first selection is:

`P(1st\text{ non-tongue twister) =}\frac{number\text{ of non-tongue twisters}}{\text{total numbe of sample space}}=(500-225)/(500)=(275)/(500)`

- the probability associated with the second selection is:

`P(2nd\text{ non-tongue twister) =}\frac{number\text{ of non-tongue twisters AFTER 1st selection}}{\text{total numbe of sample space after 1st selection}}=(274)/(499)`

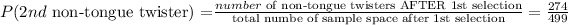
Now, the the probability that both of the two people selected from the sample can NOT twist their tongues is therefore:

`P(1st\text{ non-tongue twister) }*\text{ }P(2nd\text{ non-tongue twister)}`

Therefore:

`P(1st\text{ non-tongue twister) }*\text{ }P(2nd\text{ non-tongue twister) =}(275)/(500)*(274)/(499)=(1507)/(4990)`

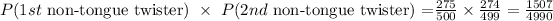
The answer is thus : 1507/4990