Let's first arrange the given data in ascending order:
0.29, 0.30, 0.37, 0.38, 0.40, 0.43, 0.43, 0.43, 0.45, 0.53, 0.54, 0.59, 0.60, 0.60, 0.61, 0.69, 0.70, 0.72, 0.73, 0.76
A.) The mean is the mathematical average of a set of two or more numbers.
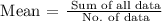
Mean = (0.29 + 0.30 + 0.37 + 0.38 + 0.40 + 0.43 + 0.43 + 0.43 + 0.45 + 0.53 + 0.54 + 0.59 + 0.60 + 0.60 + 0.61 + 0.69 + 0.70 + 0.72 + 0.73 + 0.76) / 20
Mean = 10.55/20 = 0.5275 ≈ 0.53
Therefore, the mean is 0.53
B.) The median is the middle number in a sorted, ascending or descending, list of numbers and can be more descriptive of that data set than the average.
If the number of data is an even number, the median is the sum of the two middle number.
If the number of data is an odd number, the middle number is the median.
We get,
0.29, 0.30, 0.37, 0.38, 0.40, 0.43, 0.43, 0.43, 0.45, 0.53, 0.54, 0.59, 0.60, 0.60, 0.61, 0.69, 0.70, 0.72, 0.73, 0.76
Therefore, 20 data, an even number. The two middle number is 0.53 and 0.54.
Median = (0.53 + 0.54)/2 = 1.07/2 = 0.535 ≈ 0.54
Therefore, the median is 0.54
B.) The mode is the value that appears most frequently in a data set. A set of data may have one mode, more than one mode, or no mode at all.
We get,
0.29, 0.30, 0.37, 0.38, 0.40, 0.43, 0.43, 0.43, 0.45, 0.53, 0.54, 0.59, 0.60, 0.60, 0.61, 0.69, 0.70, 0.72, 0.73, 0.76
The most frequent data is only 0.43
Therefore, there is only 1 mode.