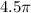Step 1. The radius of the circle is:
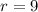
Required: Find the length of the arc.
Note: The angle formed by the arc is a right angle of 90°:
Step 2. We will start by remembering the formula to find the circumference or perimeter of a circle:
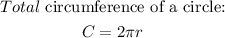
And since here the blue arc covers a 90° angle, it means that it represents one-fourth of a circle. Therefore, the arc is only 1/4 of the circumference:
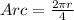
Step 3. Substituting the known value of r into our equation for the arc:
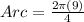
Solving the operations:
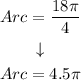
The length of the arc in terms of pi is:
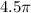
Answer: