Question

Find the equation for a line that passes through the point (4,8) and intercepts the x axis at -12.Make a sketch of its graph and label it "Line L". Be sure to label the increments on the x and y axis of your graph.Create and write down an equation for a line parallel to Line L. Graph this parallel line.Create and write down an equation for a line perpendicular to Line L. Graph this perpendicular line.

Answer 1

We are given two points through which a line passes: (4, 8) and the interception with the x-axis at x=-12. It corresponds to the point (-12, 0).

The point-slope equation of a line is:

`y-k=m(x-h)`

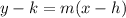
Where m is the slope and (h, k) is one given point of the line.

We can use any of the two given points, but we must calculate the slope by using the formula:

`m=(y_2-y_1)/(x_2-x_1)`

Where (x1,y1) and (x2,y2) are the coordinates of the given points. Applying the formula:

`\begin{gathered} m=(0-8)/(-12-4) \\ \text{Operating:} \\ m=(-8)/(-16) \\ m=(1)/(2) \end{gathered}`

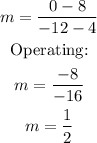
The equation of the line (we use the point (-12,0) ) is:

`\begin{gathered} y-0=(1)/(2)(x+12) \\ \text{Simplifying:} \\ y=(1)/(2)x+6 \end{gathered}`

Now we will sketch the graph by using the points (4, 8) and (-12, 0):

It's required to create a line parallel to L, but we are not told a specific point for this new line, so we select the point (-4, 0). Parallel lines have the same slope, thus the new line is:

`\begin{gathered} y-0=(1)/(2)(x+4) \\ \text{Simplifying:} \\ y=(1)/(2)x+2 \end{gathered}`

The second graph is shown along with the original line:

Finally, we must find a perpendicular line to both previous lines. We must find its slope. It can be done with the formula:

`\begin{gathered} m_2=-(1)/(m_1) \\ m_2=-(1)/((1)/(2)) \\ m_2=-2 \end{gathered}`

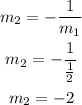
We use the same point (-4, 0) and write the equation for the perpendicular line as follows:

`\begin{gathered} y-0=-2(x+4) \\ \text{Simplifying:} \\ y=-2x-8 \end{gathered}`

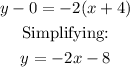
The final graph with all three lines is shown below: