Question

3x - 2y = 5 cx - 7y = 12 In the system of equations above, c is a constant and x and y are variables. For what values of c will the system of equations have no solution?

Answer 1

(D) 21/2

Step-by-step explanation:

A system of equation will have no solution if the two lines are parallel.

For two lines to be parallel, their slopes (or gradients) must be the same.

In the first equation:

`\begin{gathered} 3x-2y=5 \\ 2y=3x-5 \\ y=(3)/(2)x-5 \end{gathered}`

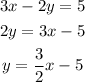
The gradient of the first line is 3/2.

In the second equation:

`\begin{gathered} cx-7y=12 \\ 7y=cx-12 \\ y=(c)/(7)x-12 \end{gathered}`

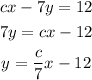
The gradient of the second line is c/7.

Since the gradients must be the same, we have that:

`\begin{gathered} (c)/(7)=(3)/(2) \\ c=(3)/(2)*7 \\ c=(21)/(2) \end{gathered}`

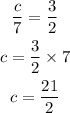
Therefore, the value of c for which the system will have no solution is 21/2.