We have the following functions, given algebraically, and as a graph:
And we have to determine if the functions are even, odd, or neither.
To determine each case, we need to recall when a function is even, or odd as follows:
• A function is odd if we have that:
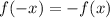
And we can say that the function is symmetric with respect to the origin.
• A function is even if we have that:
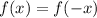
And we can say that the function is symmetric with respect to the y-axis.
Then we can conclude from the graphs that (functions r and s):
Function r
For function r, the function r graphically is not symmetric with respect to the y-axis, and neither with respect to the origin. Therefore, the function is neither odd nor even function.
Function s
The function s is symmetric with respect to the origin, that is, the function looks in the same way right side up or upside down. Then the function s is an odd function.
Function g(x)
We can analyze this function algebraically as follows:
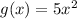
Then to determine if it is even we have:
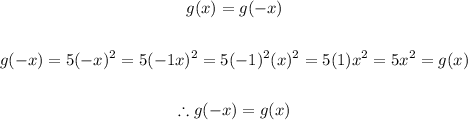
Therefore, this function is even.
We can also determine if the function is odd by using a similar procedure:
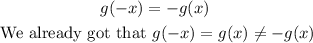
Therefore, the function is NOT an odd function.
Function h(x)
To determine if the function is even, we have:
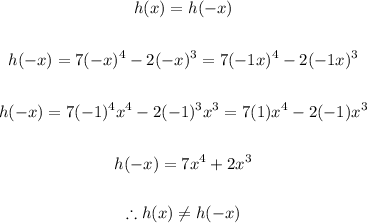
Then the function is NOT even.
Now, we have to determine if the function is odd:
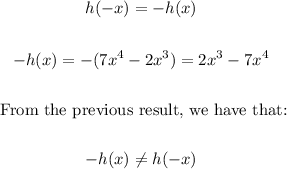
Then the function is NOT odd.
Therefore, in summary, we can conclude that:
• Function r ---> Neither
,
• Function s ---> Odd
,
• Function g(x) ---> Even
,
• Function h(x) ---> Neither