Question

Help would be nice, i’m out of school from covid

Answer 1

We are to pick from the given tiles the pairs that are associated with each functions.

Note that each of the pairs are of the form (x,y) coordinates.

(1)

`y=6^x`

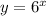
The correct tiles for this function with explanation are given as follow;

`\begin{gathered} (1,6)\text{ } \\ y\text{ = 6 when x =1 } \\ y=6^x \\ 6=6^1 \\ \text{Correct} \end{gathered}`
`\begin{gathered} (0,1) \\ y\text{ = 1 when x = 0} \\ y=6^x \\ 1=6^0 \\ \text{Correct} \end{gathered}`
`\begin{gathered} (2,36) \\ y=36\text{ when x = 2} \\ y=6^x \\ 36=6^2 \\ \text{Correct} \end{gathered}`
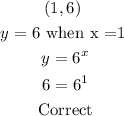
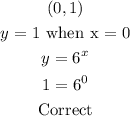
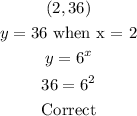
`\begin{gathered} (0.5,\sqrt[]{6)} \\ y\text{ = }\sqrt[]{6}\text{ when x = 0.5} \\ y=6^x \\ \sqrt[]{6}=6^(0.5) \\ \sqrt[]{6}=6^{(1)/(2)} \\ \sqrt[]{6}\text{ = }\sqrt[]{6} \\ \text{Correct} \end{gathered}`

For the first function, above tried tiles are the associated ones any other one different from those explained above are not associated with the fuction.

(2)

`y=\log _6x`

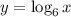
The correct tiles for this function are given as follow;

`(6,1),\text{ (1, 0), (36 ,2) and (}\sqrt[]{6\text{ }}\text{ , 0.5)}`

Let me explain or prove two out of the four tiles.

`\begin{gathered} (6,\text{ 1)} \\ y\text{ = 1 when x =6} \\ y=\log _6x \\ 1=\log _66 \\ \text{Correct} \end{gathered}`
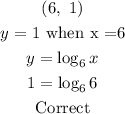
`\begin{gathered} (\sqrt[]{6},\text{ 0.5)} \\ y\text{ = 0.5 when x = }\sqrt[]{6} \\ y=\log _6x \\ 0.5\text{ =}\log _6\sqrt[]{6} \\ (1)/(2)=\log _66^{(1)/(2)} \\ \\ \frac{1}{2\text{ }}=\text{ }(1)/(2)\log _66 \\ \\ \frac{1}{2\text{ }}=\text{ }(1)/(2)\text{ x 1} \\ \\ \frac{1}{2\text{ }}=\text{ }(1)/(2)\text{ } \\ \\ \text{Correct} \end{gathered}`

You can also use the approach above to confirm the remaining two.