SOLUTION:
We are to pick from the given tiles the pairs that are associated with each functions.
Note that each of the pairs are of the form (x,y) coordinates.
(1)
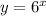
The correct tiles for this function with explanation are given as follow;
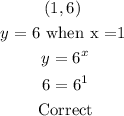
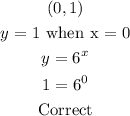
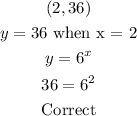
![\begin{gathered} (0.5,\sqrt[]{6)} \\ y\text{ = }\sqrt[]{6}\text{ when x = 0.5} \\ y=6^x \\ \sqrt[]{6}=6^(0.5) \\ \sqrt[]{6}=6^{(1)/(2)} \\ \sqrt[]{6}\text{ = }\sqrt[]{6} \\ \text{Correct} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wo2djpaashi596f0zy09es1ax8ejewm7de.png)
For the first function, above tried tiles are the associated ones any other one different from those explained above are not associated with the fuction.
(2)
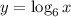
The correct tiles for this function are given as follow;
![(6,1),\text{ (1, 0), (36 ,2) and (}\sqrt[]{6\text{ }}\text{ , 0.5)}](https://img.qammunity.org/2023/formulas/mathematics/college/1bauqa85ss1pehq6zm6eabkqg1gx9pleb0.png)
Let me explain or prove two out of the four tiles.
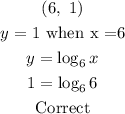
![\begin{gathered} (\sqrt[]{6},\text{ 0.5)} \\ y\text{ = 0.5 when x = }\sqrt[]{6} \\ y=\log _6x \\ 0.5\text{ =}\log _6\sqrt[]{6} \\ (1)/(2)=\log _66^{(1)/(2)} \\ \\ \frac{1}{2\text{ }}=\text{ }(1)/(2)\log _66 \\ \\ \frac{1}{2\text{ }}=\text{ }(1)/(2)\text{ x 1} \\ \\ \frac{1}{2\text{ }}=\text{ }(1)/(2)\text{ } \\ \\ \text{Correct} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/18eaftkl0decouui3hj925aq7gj95ebr58.png)
You can also use the approach above to confirm the remaining two.