Is my answer correct? question : prove that there is no tangent line to p(x) = 3x^(2) + 6xthat passes through the point (-1;5)

Question

is my answer correct? question : prove that there is no tangent line to
`p(x) = 3x^(2) + 6x`that passes through the point (-1;5)

Answer 1

The equation is given by:

`\begin{gathered} p(x)=3x^2+6x \\ p^(\prime)(x)=6x+6 \end{gathered}`

Slope of tangent will be:

`p^(\prime)(-1,5)=m=6(-1)+6=0`

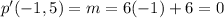
The equation of tangent is given by:

`\begin{gathered} y-5=0(x-(-1)) \\ y=5 \end{gathered}`

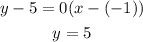
The line is tangent if it touches the curve at a single point:

Substitute P(x)=5 to get:

`\begin{gathered} 3x^2+6x=5 \\ 3x^2+6x-5=0 \end{gathered}`

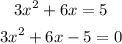
The line is tangent if the discriminant is 0 so it follows:

`\Delta=6^2-4(3)(-5)=96>0`

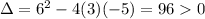
Hence the roots of the equation are real and unequal.

Hence there is no tangent that can be drawn from point (-1,5) to the given curve.