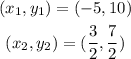we are given the following system of equations:
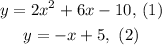
To solve this system of equations we will use the method of substitution by substituting the value of "y" from equation (2) into equation (1), like this:
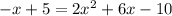
now, we will move all the variables to the right side of the equation by adding "x" on both sides:
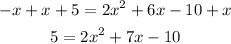
Now we will move the constants to the right side of the equation by subtracting 5 on both sides:
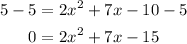
To solve this equation, we will factor the expression on the right side, first by multiplying and dividing by 2
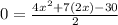
Now we will factor, like this:
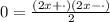
In the spaces, we need to find two numbers which sum is 7 and product are -30, these numbers are 3 and 10, since:

Replacing we get:
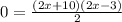
Now we simplify the expression, like this:
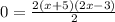
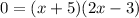
Now, we equal each of the products expressions to zero, like this:
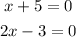
Now we solve for "x" in each one of them:
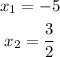
Therefore, the two solutions for "x" are -5 and 3/2. To find the "y" values we replace these values in equation (2). Replacing the first value of "x"
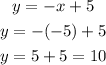
replacing the second value of "x", we get:

Therefore, the solutions of the system are: