Question

A group has at most 200 to spend on food, Sandwiches cost 15 and drinks cost $3. Write an inequality to describe the situation

Answer 1

`15x+3y\leq200`

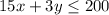
Step-by-step explanation

Step 1

let x represents the number of sandwiches

let y represents the number of drinks

hence,

the cost of the sandwich would be

`\begin{gathered} tota\text{l cost of sandwiches= 15}\cdot x \\ tota\text{l cost of sandwiches=}15x \end{gathered}`

and

`\begin{gathered} tota\text{l cost of DRINKS= 3}\cdot y \\ tota\text{l cost of DRINKS=}3y \end{gathered}`

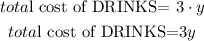
so, The total cost is

`\begin{gathered} \text{total cost = cost of sandwiches+cost of drinks} \\ \text{replace} \\ \text{total cost= 15x+3y} \end{gathered}`

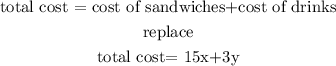
so, we have an equation for the total cost

Step 2

we are told that the group can spend at most $200, in other words the total cost must be equal or smaller than 200, in math term it is

`\begin{gathered} total\cos t=15x+3y \\ total\cos t\leq200 \\ \text{therefore} \\ 15+3y\leq200 \end{gathered}`

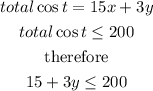
so, the answer is

`15+3y\leq200`

I hope this helps you