Question

how fast is the angle of depression of the telescope changing when the boat is 260 meters from shore? Round any intermediate calculations to no less than six decimal places, and round your final answer to four decimal places

Answer 1

We can draw the problem as follows:

So, in order to find how fast the angle of depression of the telescope is changing, we need to use the formula:

`(\Delta\theta)/(\Delta t)=((tan^(-1)(40)/(260-15))-(\tan ^(-1)(40)/(260)))/(1s)`

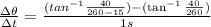
Notice that, in the first drawing, we have:

`\tan \theta=(40)/(260)\text{ }\Rightarrow\theta=\tan ^(-1)(40)/(260)`

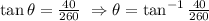
And the same happens for the second drawing, but we use 260 - 15 as the denominator (since the boating is approaching at a speed of 15m/s).

So, we have:

`\begin{gathered} (\Delta\theta)/(\Delta t)=((tan^(-1)(40)/(245))-(\tan ^(-1)(40)/(260)))/(1s) \\ \\ (\Delta\theta)/(\Delta t)\cong(0.1618374-0.1526493)/(1s) \\ \\ (\Delta\theta)/(\Delta t)\cong(0.0091881)/(s) \\ \\ (\Delta\theta)/(\Delta t)\cong0.0092 \end{gathered}`

Therefore, the answer is:

0.0092 rad/s