An irrational number is a number which cannot be expressed as the quotient of two integers.
The constant:

Is an irrational number. So, the number:
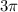
Must also be an irrational number. This is because if it was a rational number, then there would be two integers a and b such that:
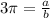
Then, we would be able to write the constant π as the quotient of a and 3b:

which is not possible, since π is an irrational number.
Therefore, 3π is irrational.