Question

A boat sails on a bearing of 79° for 145 miles and then turns and sails 228 miles on a bearing of 191°. Find the distance of the boat from its starting point . (Round to the nearest integer as needed.)

Answer 1

The given problem can be exemplified in the following diagram:

The trajectory of the boat can be divided into two distinct right triangles, as shown in the figure. The difference between each of the sides of the right triangle form another right triangle that will allow us to determine the total distance using the Pythagorean theorem.

`a=145\cos 79-228\cos 191`

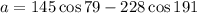
Solving the operation:

`a=251.5`

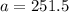
Now using the sine function:

`b=145\sin 79-228\sin 191`

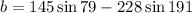
Solving the operations:

`b=185.8`

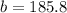
This can be exemplified in the following diagram:

Using the Pythagorean theorem:

`h^2=a^2+b^2`

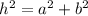
Replacing the values:

`h^2=(251.5)^2+(185.8)^{2^{}}`

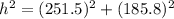
Solving the operations:

`h^2=97773.89`

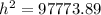
Taking square root to both sides:

`\begin{gathered} h=\sqrt[]{97773.89} \\ h=312.6\approx313 \end{gathered}`

Therefore, the total distance is 313 miles.