Step 1 - write out the formula for computing the monthly payment d
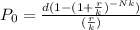
Where

Step 2 - write out the given values and substitute them into the formula:
In this case,
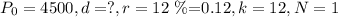
Therefore,
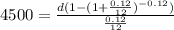
Dividing the numbers, we have
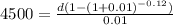
Multiplying both sides by 0.01, we have:
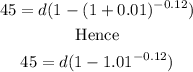
Therefore,
![undefined]()