Question

Jolyn's points per basketball game are normally distributed with a standard deviation of 7 points. If Jolyn scores 48points, and the Z-score of this value is 3, then what is her mean points in a game? Do not include the units in youranswer. For example, if you found that the mean is 33 points, you would enter 33.

Answer 1

The variable of interest is X: Jolyn's points per basketball game.

This variable has a normal distribution with mean μ and standard deviation δ=7 points.

In one game Jolyn scored X=48 points, the Z-score that corresponds to this value of the variable is Z=3.

The standard normal distribution is derived from the normal distribution, to construct it, you have to subtract the mean from the value of the variable and divide it by the standard deviation following the formula:

`Z=(X-\mu)/(\sigma)`

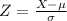
To determine the mean value of the variable, you have to write the formula for μ.

-The first step is to pass δ to the left side of the equation by applying the opposite operation to both sides of it:

`\begin{gathered} Z\cdot\sigma=\sigma((X-\mu)/(\sigma)) \\ Z\cdot\sigma=X-\mu \end{gathered}`

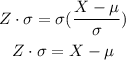
-Next, subtract X from both sides of the equal sign to pass it to the left side:

`\begin{gathered} (Z\cdot\sigma)-X=X-X-\mu \\ (Z\cdot\sigma)-X=-\mu \end{gathered}`

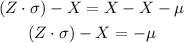
-Now, multiply both sides by (-1) to change the sign of μ

`\begin{gathered} (-1)\lbrack(Z\cdot\sigma)-X\rbrack=(-1)(-\mu) \\ -(Z\cdot\sigma)+X=\mu \end{gathered}`

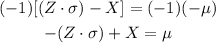
You can order the values:

`\mu=X-(Z\cdot\sigma)`

Now that we have determined the expression for μ, replace it with the known data X=48, Z=3, and δ=7 to calculate the mean:

`\begin{gathered} \mu=X-(Z\cdot\sigma) \\ \mu=48-(3\cdot7) \\ \mu=48-21 \\ \mu=27 \end{gathered}`

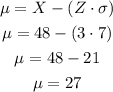
Jolyn's mean points in a game are μ=27