Question

A bicycle travelling at speed v requires frictional force F to turn on an unbanked road. How much frictional force would it require to make the same turn at a speed of 2v?a. F/4b. F/8c. 4Fd. F/2e. 2Ff. 8Fg. F

Answer 1

Given:

The required frictional force to turn on a road is,

`F`

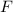
while the bicycle is moving at a speed of

`v`

To find:

The frictional force required to make the same turn at a speed of 2v

Step-by-step explanation:

The required frictional force should be equal to the centrifugal force. So, we can write,

`F=(mv^2)/(r)`

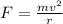
Now, for the speed 2v, the frictional force is,

`\begin{gathered} F^(\prime)=(m(2v)^2)/(r) \\ =(m*4v^2)/(r) \\ =(4mv^2)/(r) \\ =4F \end{gathered}`

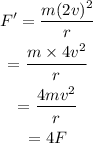
Hence, the required force is 4F.