Question

A card company claims that 70% of all American college students send a card to their father on Father's Day. Suppose you plan to gather your own data to test this claim. You select a SRS of 150 American college students to determine the proportion of them who sent a card to their mother on Mothers Day. Your sample indicates that 60% of the sample sent a card. Is the card company's claim valid? Justify your answer using a 0.05 significance level.

Answer 1

Given data

Step 1: State the null and alternative hypothesis

`\begin{gathered} \mu=70\text{ \% = 0.7} \\ \text{Hence H}_0=0.7 \end{gathered}`
`H_(\alpha)\\e0.7`

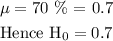
Step 2: Declare the significance level

• sample size (n) = 150

,

• Get the standard deviation (s)

`\begin{gathered} \mu=0.7 \\ 1-\mu=1-0.7=0.3 \\ \end{gathered}`

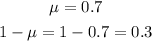
`\begin{gathered} s=\sqrt[]{(\mu(1-\mu))/(n)} \\ \\ s=\sqrt[]{\frac{0.7\text{ x 0.3}}{150}} \\ \\ s=0.037 \end{gathered}`

Step 3: Find the significance level

`\begin{gathered} Z=\frac{\bar{x}-\mu}{s}=(0.6-0.7)/(0.037) \\ \\ Z=-2.703 \end{gathered}`

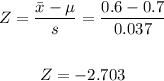
Step 4: Find the corresponding probability of the Z-score, since it is two-tailed test, then

`\begin{gathered} P(Z<-2.7)+P(Z>2.7) \\ \Rightarrow0.0035+0.0035 \\ \Rightarrow0.007 \end{gathered}`

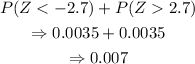
Conclusion

Since the P-value of the z-score is less than the P-value of the alpha level

That is 0.007 < 0.05, therefore the null hypothesis will be rejected

Therefore, we can conclude that the card company's claim is invalid