Question

Determine whether the two triangles are similar. Justify your answer using a similarity postulate (AA, SAS, and SSS)

Answer 1

Notice that if we write the proportions according to the length of the sides of each triangle, we get:

`(15)/(55)=(33)/(121)`

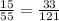
if we do cross product with the denominators, we get the following:

`\begin{gathered} (15)/(55)=(33)/(121) \\ \Rightarrow15\cdot121=33\cdot55 \\ \Rightarrow1815=1815 \end{gathered}`

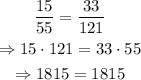
since we get 1815=1815, which is always true, we can conclude by the SSS similarity postulate that triangles DEF and SRT are similar