Given:
Plan A
- no monthly fee
- $0.06 per minute of use
Plan B
- $6 monthly fee
- $0.04 per minute of use
Find: number of minutes where the cost of Plan A > cost of Plan B
Solution:
Let's create an equation for each plan's cost per month.
Let m = number of minutes of phone use
Plan A's cost = 0.06m
Plan B's cost = 0.04m + 6
For the inequality cost of Plan A > cost of Plan B, this can be written as:

From this, we can solve for "m".
Subtract 0.04 m on both sides of the inequality.
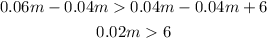
Divide both sides of the equation by 0.02.

Therefore, when the number of minutes of phone use is greater than 300, the monthly cost of Plan A will be more than the monthly cost of Plan B.