Question

50. How many solutions are there for the system y=3x-4 y-2x=6?A. 3B. 2C. 1D. 0

Answer 1

The given system is

`\begin{gathered} y=3x-4\rightarrow(1) \\ y-2x=6\rightarrow(2) \end{gathered}`

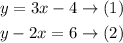
Since the coefficients of x are different in both equations

Then this system has only 1 solution

Let us check that by solving the 2 equations

Substitute y in equation (2) by equation (1)

`\begin{gathered} (3x-4)-2x=6 \\ 3x-4-2x=6 \end{gathered}`

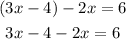
Add the like terms on the left side

`\begin{gathered} (3x-2x)-4=6 \\ x-4=6 \end{gathered}`

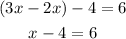
Add 4 to each side

`\begin{gathered} x-4+4=6+4 \\ x=10 \end{gathered}`

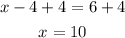
Substitute x in equation (1) by 10 to find y

`\begin{gathered} y=3(10)-4 \\ y=30-4 \\ y=26 \end{gathered}`

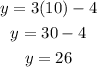
The system has the solution (10, 26)

It is only 1 solution

The answer is C