Let P be the population of the city at any year (t).
Given that the rate of increase of population is 2.4%, so the population in different years is given by,
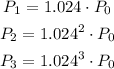
So the general expression representing the population in any nth year is given by,
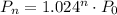
Given that the initial population is 36,314
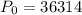
Substitute this value in the general expression,
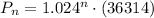
(a)
Note that the year 2020 is considered as the base year (n=0).
So the value of 'n' corresponding to the year 2025 will be,
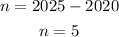
Then, the population in the year 2025 is calculated as,
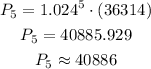
Thus, the city's population will be approximately 40886 in the year 2025.
(b)
Let N be the number of years it takes the population to double itself,
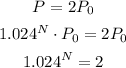
Taking logarithms on both sides,
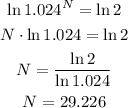
Note that the required number of years is a little more than 29 years, so we have to go for the upper estimate of N, as N cannot be in a fraction.
Therefore, it will take 30 years for the population to double itself.