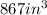Question

Find the volume of a pyramid with a square base, where the side length of the base is 17 in and the height of the pyramid is 9 in. Round your answer to the nearest tenth of a cubic inch Answer: in Submit Answer attempt 1 out of 2

Answer 1

Knowing that it is a Regular square pyramid, you can use the following formula for calculate its volume:

`V=(Bh)/(3)`

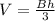
Where "B" is the area of the base and "h" is the height of the pyramid.

The area of square can be found with this formula:

`A=s^2`

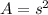
Where "s" is the length of any side of the square.

In this case you know that the side length of the base is:

`s=17in`

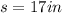
Therefore, its area is:

`B=(17in)^2=289in^2`

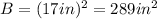
According to the information given in the exercise:

`h=9in`

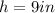
Knowing "B" and "h", you can substitute values into the formula and then evaluate, in order to calculate the volume of this pyramid. This is:

`\begin{gathered} V=((289in^2)(9in))/(3) \\ \\ V=(2601in^3)/(3) \\ \\ V=867in^3 \end{gathered}`

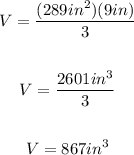
The answer is:

`867in^3`