gof means that we must first evalute f at x and next evalute the result in g.
In our case,
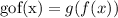
By taking into account that f(x)=3x-1 and g(x)=4x^2+9, we have
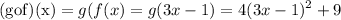
In summary,
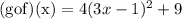
Now, we must substitute x=-2 in this lat equation, It yields
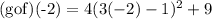
hence, we obtain,
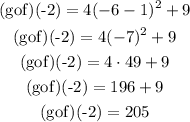
Hence, the answer is 205