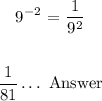Question

What is the value of
`9 {}^(6) * {9}^(4) \\ {9}^(12)`

Answer 1

We will investigate how to simplify fractions involving powers of similar bases.

The following fraction is given for simplification:

`(9^6\cdot9^4)/(9^(12))`

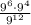
When we have fraction with numerator and denominator have similar digits as basis; however, different powers we apply power rules of multiplication and division as follows:

`\begin{gathered} \text{Multiplication: x}^a\cdot x^b=x^(a+b) \\ \\ Division\text{: }(x^a)/(x^b)=x^(a-b) \end{gathered}`

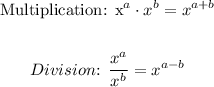
Using the above rules we will simplify the given expression. We will keep in mind the order of priority for mathematical opperations i.e ( PEMDAS ).

We will first multiply out the result in the numerator using the multiplication power rule as follows:

`\begin{gathered} (9^(6+4))/(9^(12)) \\ \\ (9^(10))/(9^(12)) \end{gathered}`

Then we will apply the division power rule to the above resulting expression and simplify further as follows:

`\begin{gathered} \frac{9^(10)}{9^(12)\text{ }}=9^(10-12) \\ \\ 9^(-2)\text{ } \end{gathered}`

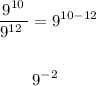
Then we will apply the negative exponent power rule. Where any negative exponent can be converted to positive exponent by reciprocating the base as follows:

`\text{Negative Exponent Rule: x}^(-a)\text{ = }(1)/(x^a)`

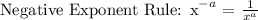
Apply the above rule:

`\begin{gathered} 9^(-2)\text{ = }(1)/(9^2) \\ \\ (1)/(81)\ldots\text{ Answer} \end{gathered}`