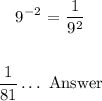We will investigate how to simplify fractions involving powers of similar bases.
The following fraction is given for simplification:
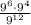
When we have fraction with numerator and denominator have similar digits as basis; however, different powers we apply power rules of multiplication and division as follows:
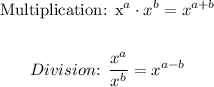
Using the above rules we will simplify the given expression. We will keep in mind the order of priority for mathematical opperations i.e ( PEMDAS ).
We will first multiply out the result in the numerator using the multiplication power rule as follows:

Then we will apply the division power rule to the above resulting expression and simplify further as follows:
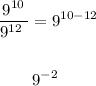
Then we will apply the negative exponent power rule. Where any negative exponent can be converted to positive exponent by reciprocating the base as follows:
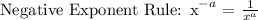
Apply the above rule: