Question

Can someone please explain this to me? I have a lot of trouble with two columns proofs

Answer 1

We are to write two columns proofs for the given geometry problem.

There are two ways to express the proof to the given problem. We will investigate each of them separately:

A two coloumn proof is categorized into " STATEMENTS " and " REASONS ".

Where, statements gives us the relations between angles, sides, and/or lines with the help of some standard mathematical symbols. Reasons gives us the explanantion behind the statements made.

Method 1:

`\text{\textcolor{#FF7968}{Statement: }}\text{m }\angle\text{ 1 =}\text{\textcolor{#FF7968}{ }}\text{62}\text{\textcolor{#FF7968}{ }}\text{degrees}`
`\text{\textcolor{#FF7968}{Reason: }}\text{Given}`

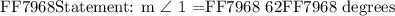
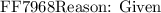
Now, we have to recall laws of intersecting lines. When two lines intersect ( l and t ) they always make up 4 angles with two sets of complementary angles.

Amoung these 4 angles ( 1 , 2 , 3 , 4 ) there are two set of vertically opposite angles that are equal in magnitude.

Using the given image, we see that the sets of vertically opposite angles are 1 : 4 AND 2 : 3.

So on the basis of law of angles for two intersecting lines we can make our next statement as follows:

`\text{\textcolor{#FF7968}{Statement:}}\text{ }\angle1\text{ = }\angle4\text{ = 62 degrees}`
`\text{\textcolor{#FF7968}{Reason:}}\text{ Vertically opposite angles}`

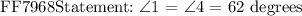
Method 2:

`\text{\textcolor{#FF7968}{Statement: }}\text{m }\angle\text{ 1 =}\text{\textcolor{#FF7968}{ }}\text{62}\text{\textcolor{#FF7968}{ }}\text{degrees}`
`\text{\textcolor{#FF7968}{Reason}}\text{: Given}`

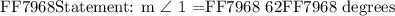
For this we will recall the sum of of supplementary angles for a line is given as:

`\begin{gathered} LineL\colon180\text{ = }\angle\text{ 1 + }\angle\text{ 2} \\ AND \\ LineL\colon180\text{ = }\angle\text{ 3 + }\angle\text{ 4} \\ AND \\ t\colon\text{ 180 = }\angle\text{2 + }\angle4 \\ \text{AND} \\ t\colon\text{ 180 = }\angle\text{1 + }\angle3 \end{gathered}`

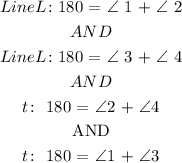
Hence, the statement 2 would be:

`\begin{gathered} LineL\colon\angle2\text{ = 180 - }\angle1=118degrees\text{ } \\ OR \\ Linet\colon\angle3\text{ = 180 - }\angle1\text{ = 118 degrees} \end{gathered}`
`\text{\textcolor{#FF7968}{Reason:}}\text{ Sum of supplementary angles is always 180 degrees for two intersecting lines.}`

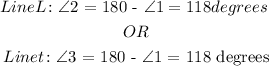
Now, we appl