Solution:
The compound interest formula is
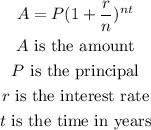
If you sign up for an account now, you get 2 years of 12% annual interest rate compounded monthly, i.e.
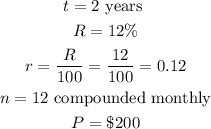
The amount after the first two years is

The amount after the first two years is $253.95 (nearest cent)
For the rest of the time, i.e. the next 2 years,
Where

The amount for after 4 years will be
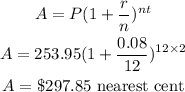
Hence, the amount after 4 years is $297.85 (nearest cent)