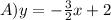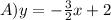
Step-by-step explanation
Step 1
find the slope of the given line
you can find the slope using:

P1 and P2 are 2 known points of the line
then,let
P1(0,-1)
P2(3,1)
replace
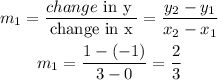
Step 2
Now, 2 lines are perpendicular if the product of their slopes equals - 1
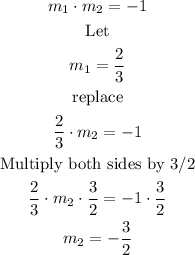
Hence, the line we are looking for has a slope of -3/2
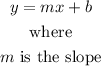
the number with the variable is the slope, so find in the optiions the answer with :

so, the answer is