We have that the scores of students on the SAT college entrance examination had a normal distribution with the following parameters:
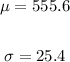
And we need to find the following information:
1. The probability that a student is randomly chosen from all those taking the test scores 559 or higher.
2. If we take a simple random sample of 30 students, we need to find:
• The mean of the sampling distribution
,
• The standard deviation of the sampling distribution
,
• The z-score that corresponds to the mean score x-hat = 559
,
• The probability that the mean score x-hat of these students is 559 or higher.
To find those answers, we can proceed as follows:
1. To find the probability that a student is randomly chosen from all those taking the test scores 559 or higher, we can find that probability by using the z-score associated with x = 559 as follows:
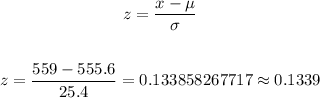
And now, we can use the cumulative standard normal distribution table to find the cumulative probability for z = 0.1339. Then we have:
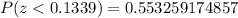
Since we need test scores of 559 or higher, then we have:
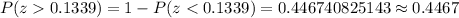
Therefore, the probability for test scores of 559 or higher is about 0.4467.