Question

Use two points to enter an equation for the function. Give your answer in the form a(b)*. In the eventthat a = 1, give your answer in the form (b)*.The equation is f(x) =

Answer 1

`f(x)=14((1)/(7))^x`

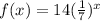
Explanations:

The standard exponential equation is expressed as:

`y=a(b)^x`

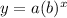
where:

• a is the ,intercept

,

• b is the ,rate, (whether growth or decline)

Since we have several coordinate points from the table, we can make use of the coordinate points (3, 2/49) and (4, 2/343)

Set up a simultaneous equation using these coordinates as shown:

`\begin{gathered} (2)/(49)=ab^3 \\ (2)/(343)=ab^4 \end{gathered}`

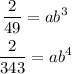
Divide both equations to have:

`\begin{gathered} (((2)/(49)))/(((2)/(343)))=(ab^3)/(ab^4) \\ \frac{\cancel{2}}{49}*\frac{343}{\cancel{2}}=(b^3)/(b^4) \\ (343)/(49)=b^(3-4) \\ 7=b^(-1) \\ b=(1)/(7) \end{gathered}`

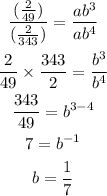
Substitute the value of x, y, and b into any of the equations;

`\begin{gathered} (2)/(49)=a((1)/(7))^3 \\ (2)/(49)=((1)/(343))a \\ (2)/(49)=(a)/(343) \\ 49a=2*343 \\ 49a=686 \\ a=(686)/(49) \\ a=14 \end{gathered}`

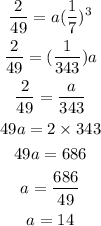
Get the required exponential function

`\begin{gathered} y=a(b)^x \\ y=14((1)/(7))^x \end{gathered}`

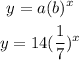
Hence the required exponential equation is f(x) = 14(1/7)^x