Question

a fruit company delivers its fruit in two types of boxes large and small A delivery of two large boxes in 3 small boxes has a total weight of 78 kg A delivery of 6 large boxes and five small boxes has a total waste of 180 kg how much does each type of box weigh

Answer 1

Let the weight (in kg) of a large box be 'x' and the weight of a small box be 'y'.

Given that the weight of 2 large boxes and 3 small boxes is 78 kg,

`2x+3y=78`

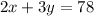
Also given that the weight of 6 large boxes and 5 small boxes is 180 kg,

`6x+5y=180`

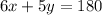
Here we will apply the Elimination Method to solve both the equations.

Consider the three times the first equation being subtracted from the second equation,

`(6x+5y)-3(2x+3y)=180-3(78)\Rightarrow6x+5y-6x-9y=180-234`

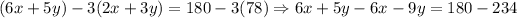
Simplify the terms,

`-4y=-54\Rightarrow y=(54)/(4)=13.5`

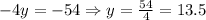
Substitute this value in the first equation,

`2x+3(13.5)=78\Rightarrow2x=78-40.5\Rightarrow2x=37.5\Rightarrow x=18.75`

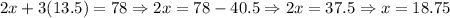
Thus, the larger box weighs 18.75 kg while the small box weighs 13.5 kg