To solve this problem, we have to use Hooke's Law.
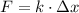
Where k is the constant of the spring, and x is the displacement we have to find.
According to the problem, the force is 7 times the runner's weight, which means
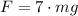
Where m = 65 kg and g = 9.8 m/s^2. Let's find this force.
![\begin{gathered} F=7\cdot65\operatorname{kg}\cdot9.8\cdot(m)/(s^2) \\ F=4459N \end{gathered}]()
Then, we use Hooke's Law to find the displacement.
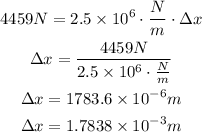
But, we have to find the displacement in millimeters. So, let's divide by 1000.
![\begin{gathered} \Delta x=(1.7838*10^(-3))/(1000)mm \\ \Delta x\approx0.002\operatorname{mm} \end{gathered}]()
Therefore, the runner's Achilles tendon will stretch 0.002 mm.