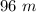1 Answer

Yosem · Answer 1 · 2023-09-23T10:19:16+0000

Given that:

- The length of the rectangle is 5 times its width:

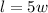
- Its area is:

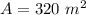
$A=320\text{ }m^2$

You need to remember that the formula for calculating the area of a rectangle is:

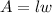
Where "l" is the length and "w" is the width.

Then, in this case, you can set up that:

Solve for "w" in order to find the width:

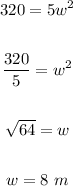
$\begin{gathered} 320=5w^2 \\ \\ (320)/(5)=w^2 \\ \\ √(64)=w \\ \\ w=8\text{ }m \end{gathered}$

Knowing the width, you can find the length:

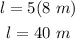
$\begin{gathered} l=5(8\text{ }m) \\ l=40\text{ }m \end{gathered}$

The formula for calculating the perimeter of a rectangle is:

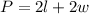
Where "l" is the length and "w" is the width.

Then, knowing the values of "l" and "w", you can substitute them into the formula and then evaluate, in order to find the perimeter of the rectangle:

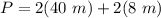
$P=2(40\text{ }m)+2(8\text{ }m)$
$P=80\text{ }m+16\text{ }m$
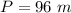
$P=96\text{ }m$

Hence, the answer is:

$96\text{ }m$

Please log in or register to add a comment.