Given:
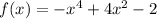
To determine the maximum turns of the given function in its graph, we first note that the maximum number of turning points of a polynomial function is always one less than the degree of the function. Based on the given function, the degree is 4, so the turning points must be:

We can double check this by graphing the function as shown below:
As we can see, there are 3 turns in its graph. Therefore, the answer is: D. 3