Question

g(x) = 2x² - 20x + 54 1. Does the function have a minimum or maximum value? 2. What is the function's minimum or maximum value? 3. Where does the minimum or maximum value occur?

Answer 1

1.

Differentiate the function with respect to x.

`\begin{gathered} (d)/(dx)g(x)=(d)/(dx)(2x^2-20x+54) \\ g^(\prime)(x)=4x-20 \end{gathered}`

For maximum and minimum value first derivative of function is equal to 0.

Evaluate the value of x by equate the first derivative of function to 0.

`\begin{gathered} 4x-20=0 \\ 4x=20 \\ x=5 \end{gathered}`

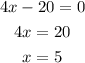
Differentiate the first derivative of function with respect to x to obtain second derivative of function.

`\begin{gathered} (d)/(dx)g^(\prime)(x)=(d)/(dx)(4x-20) \\ =4 \end{gathered}`

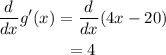
The second derivative of function is 4, which is more than 0 so x = 5 corresponds the minimum value of function.

The function has minimum value.

2.

Substitute 5 for x in the equation to obtain the minimum value of function.

`\begin{gathered} g(5)=2(5)^2-20\cdot5+54 \\ =50-100+54 \\ =4 \end{gathered}`

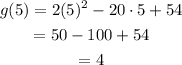
Thus, minimum value of function is 4.

3.

The minimum value of function occur at x = 5.