This question is a simultaneous equation having a quadratiic equation above and a linear equation below.
substitute the value of y in equation 2 for y in equation 1
recall y = 2x + 10 ( equation 2 )
2x + 10 = x2 - 3x -4 ( since y = 2x + 10 )
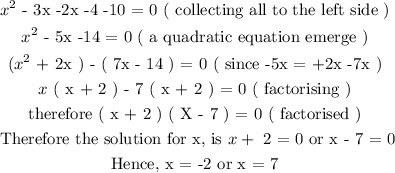
Having gotten the two values of x, we see that -2 is in the x position in the options given to us but 7 was ignored. Therefore we shall use x = -2 to find the value of y in equation 2
Recall, y = 2x + 10 ( equation 2 )
thus, y = 2 ( -2 ) + 10 ( since x = -2 )
hence, y = -4 + 10 ( since 2 x -2 = _4 )
so, y = +6
finally, x = -2 and y = 6. the best coordinate is ( -2, 6 )