Question

If is an angle in standard position and its terminal side passes through the point(5,12), find the exact value of sin 0 in simplest radical form.

Answer 1

Given the angle, θ is an angle in standard position

the terminal side passes through the point (5,12)

So,

`\begin{gathered} x=5,y=12 \\ \\ \end{gathered}`

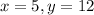
this means: opposite side = y = 12

Adjacent side = x = 5

We will find the hypotenuse (h) using the Pythagorean theorem

So,

`\begin{gathered} h^2=x^2+y^2=5^2+12^2=25+144=169 \\ h=\sqrt[]{169}=13 \end{gathered}`

So,

`\begin{gathered} \sin \theta=(opposite)/(hypotenuse) \\ \\ \sin \theta=(y)/(h) \\ \sin \theta=(12)/(13) \end{gathered}`

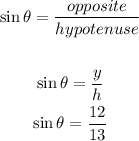
So, the answer will be: 12/13